
No rotation or reflection, just a scaled (and perhaps translated – depends on the transformation origin) copy. Well, the rotation isn’t needed either: Congruent triangles lined up. In the previous attempt it appeared the reflection part of the congruency wasn’t needed. The congruency consists of a scaling and a rotation operation only. Bisecting △ABC and expanding one part so it becomes an isosceles triangle. Here’s another, even simpler one, arriving at two triangles with two equal angles, therefor congruent. So now we have congruent triangles with x and b in one triangle and y and c in the other. The two coloured triangles have two angles in common (indicated with open and closed discs) and so are congruent. Second attempt: One congruency less Bisecting △ABC and expanding one part so it becomes congruent with the other.Īnother possibility is to extend △ABD with the isosceles triangle △BDE as above. It’s not complicated, but it requires too many steps.
ANGLE BISECTOR THEOREM PROOF PC
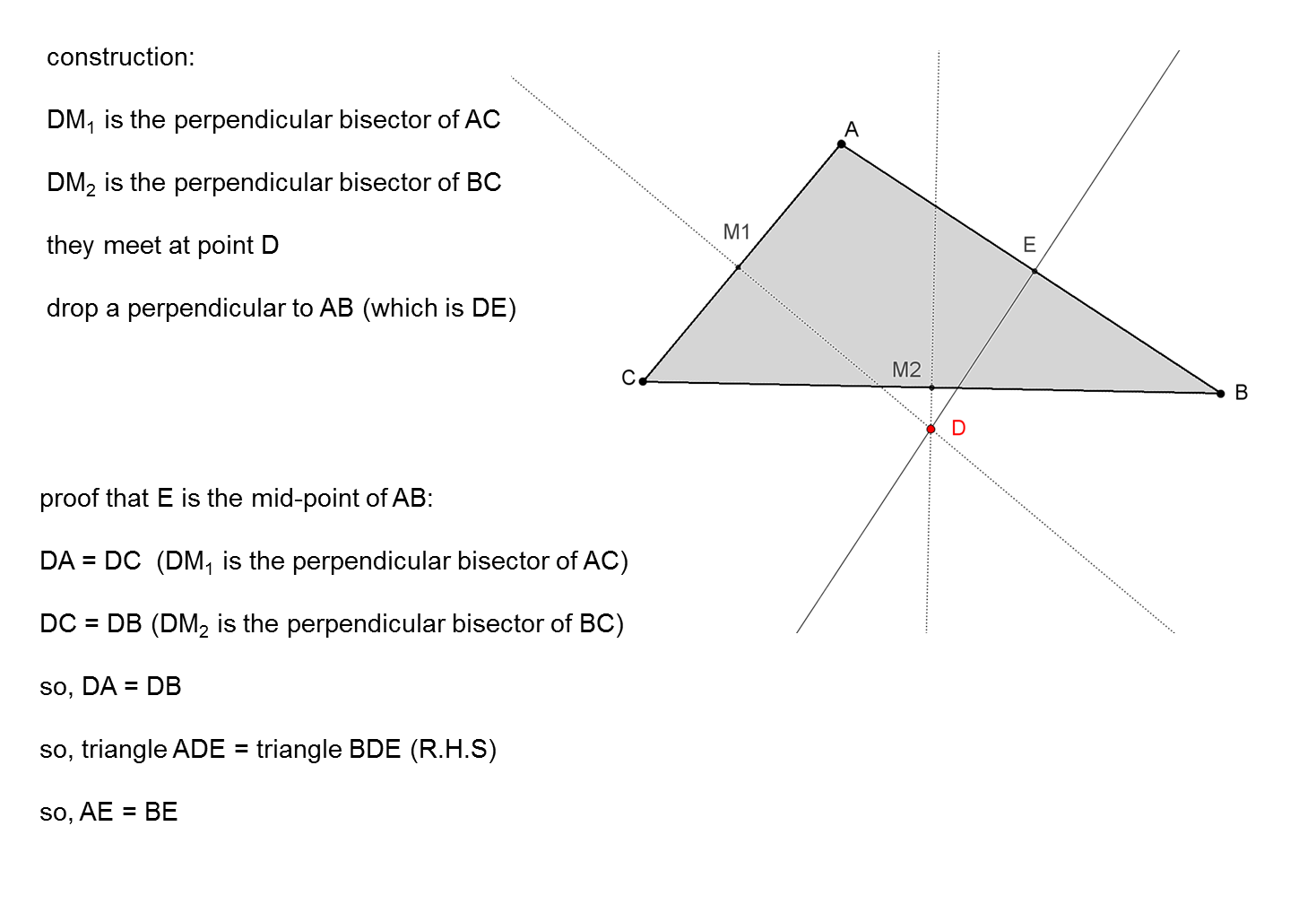
From these it follows that x : y = PC : BR = b : c. There are two pairs of congruent triangles: △ABR (the large triangle containing all geometry) to △APC (the little one crouching at the top) and △PCQ to △RBQ (the green ones). Constructing triangles, with several congruencies. Use compass and ruler (if you like) to construct points P, Q and R. First attempt: Pairs of congruent triangles And from there, effortlessly I hope, write down the proof if anyone needs it. My interest however is to find a construction that makes immediately clear that the theorem holds. Illustrating the theorem with a measurement check. So my drawing is not so bad in that respect.
In the drawing below, measuring in millimeters, I found b/x = 32/25 (= 1.28), while c/y = 61/48, which is roughly1.27. This means that if b is for example twice the length of x, then c is twice the length of y.

The Angle Bisector Theorem states that the ratio x : b equals the ratio y : c. The bisector divides the opposite line segment in a part of length x and a part of length y.
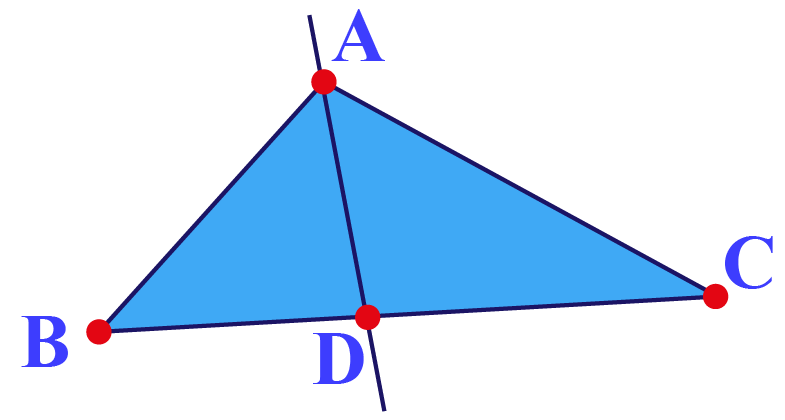
Let’s divide the angle at point A in half.


 0 kommentar(er)
0 kommentar(er)
